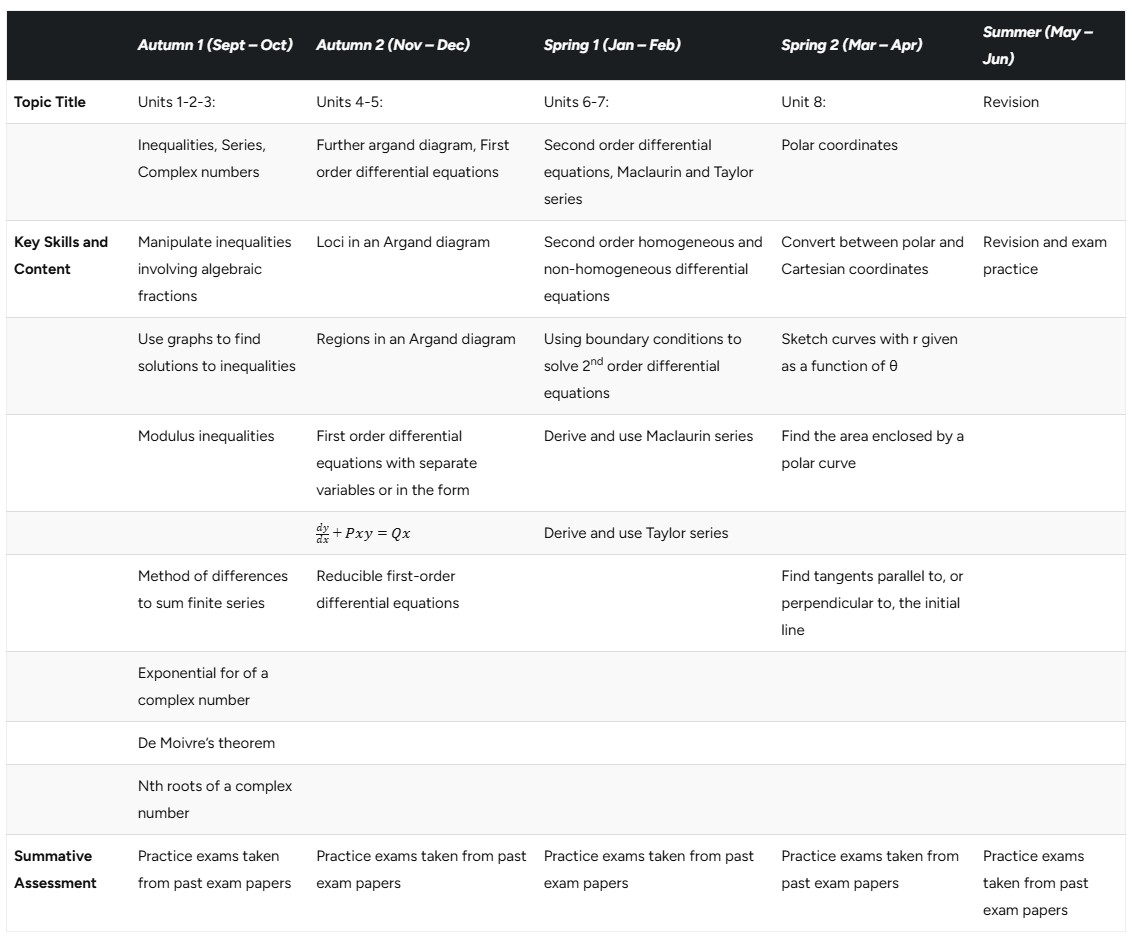
Curriculum Overview (Further Maths – Further Pure 2 – Year 13)

	Autumn 1 (Sept – Oct)	Autumn 2 (Nov – Dec)	Spring 1 (Jan – Feb)	Spring 2 (Mar – Apr)	Summer (May – Jun)
Topic Title	Units 1-2-3:	Units 4-5:	Units 6-7:	Unit 8:	Revision
	Inequalities, Series, Complex numbers	Further argand diagram, First order differential equations	Second order differential equations, Maclaurin and Taylor series	Polar coordinates
Key Skills and Content	Manipulate inequalities involving algebraic fractions	Loci in an Argand diagram	Second order homogeneous and non-homogeneous differential equations	Convert between polar and Cartesian coordinates	Revision and exam practice
	Use graphs to find solutions to inequalities	Regions in an Argand diagram	Using boundary conditions to solve 2^nd order differential equations	Sketch curves with r given as a function of θ
	Modulus inequalities	First order differential equations with separate variables or in the form	Derive and use Maclaurin series	Find the area enclosed by a polar curve
		$\frac{d y}{d x} + P (x) y = Q (x)$	Derive and use Taylor series
	Method of differences to sum finite series	Reducible first-order differential equations		Find tangents parallel to, or perpendicular to, the initial line
	Exponential for of a complex number
	De Moivre’s theorem
	Nth roots of a complex number
Summative Assessment	Practice exams taken from past exam papers	Practice exams taken from past exam papers	Practice exams taken from past exam papers	Practice exams taken from past exam papers	Practice exams taken from past exam papers

Year 13