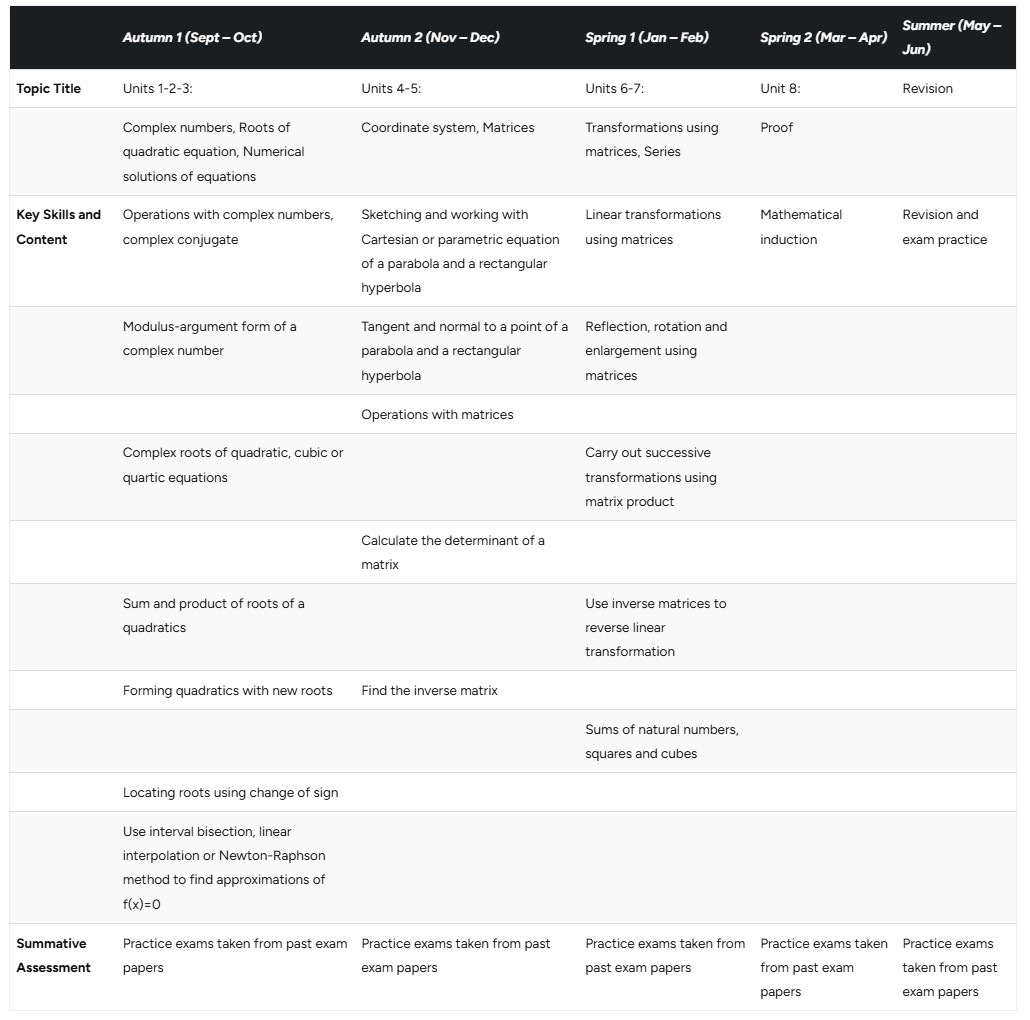
| Autumn 1 (Sept – Oct) | Autumn 2 (Nov – Dec) | Spring 1 (Jan – Feb) | Spring 2 (Mar – Apr) | Summer (May – Jun) | |
|---|---|---|---|---|---|
| Topic Title | Units 1-2-3: | Units 4-5: | Units 6-7: | Unit 8: | Revision |
| Complex numbers, Roots of quadratic equation, Numerical solutions of equations | Coordinate system, Matrices | Transformations using matrices, Series | Proof | ||
| Key Skills and Content | Operations with complex numbers, complex conjugate | Sketching and working with Cartesian or parametric equation of a parabola and a rectangular hyperbola | Linear transformations using matrices | Mathematical induction | Revision and exam practice |
| Modulus-argument form of a complex number | Tangent and normal to a point of a parabola and a rectangular hyperbola | Reflection, rotation and enlargement using matrices | |||
| Operations with matrices | |||||
| Complex roots of quadratic, cubic or quartic equations | Carry out successive transformations using matrix product | ||||
| Calculate the determinant of a matrix | |||||
| Sum and product of roots of a quadratics | Use inverse matrices to reverse linear transformation | ||||
| Forming quadratics with new roots | Find the inverse matrix | ||||
| Sums of natural numbers, squares and cubes | |||||
| Locating roots using change of sign | |||||
| Use interval bisection, linear interpolation or Newton-Raphson method to find approximations of f(x)=0 | |||||
| Summative Assessment | Practice exams taken from past exam papers | Practice exams taken from past exam papers | Practice exams taken from past exam papers | Practice exams taken from past exam papers | Practice exams taken from past exam papers |